Do you want to challenge yourself with the toughest SAT math questions? Are you curious about why these questions are so tough and how to tackle them effectively? If you aim for a perfect score, then this guide is for you. Moonpreneur has gathered the 15 most challenging SAT questions currently available. We’ll also provide you with strategies and explanations for each question. These questions are taken from official College Board SAT practice tests.
Helpful Tip: Most questions have multiple-choice answers, but some math ones require you to write the answer. Don’t worry, guessing won’t make you lose points. It’s better to guess than leave an answer blank.
Structure of SAT
The SAT is a test that lasts for three hours and has three parts:
- Reading
- Writing and Language
- Math.
When you compare it to the ACT, the SAT gives you 43% more time for each question.
Helpful Tip: The hardest SAT math questions are usually found toward the end of the multiple-choice questions or in the second half of the grid-in questions.
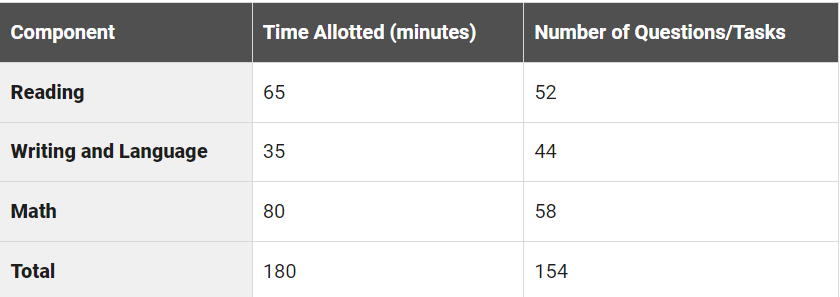
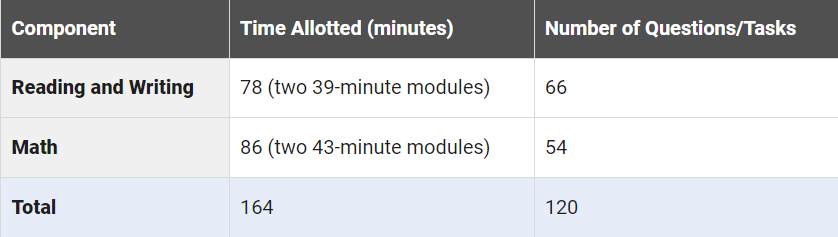
Timing
Math Test: Overview
The Math Test focuses on topics that are important for college and future jobs. They are:
- Heart of Algebra: This part is all about understanding and using linear equations and systems. Number of questions: 19.
- Problem Solving and Data Analysis: Here, you’ll get good at working with numbers and data. Number of questions: 17.
- Passport to Advanced Math: You’ll face challenging questions that involve complex equations. Number of questions: 16.
The Math Test also includes other math stuff like geometry and trigonometry that will help you in college and your career.
Number of questions in additional topics: 19
| Type of Math | No. of Questions | Percent (%) |
|---|---|---|
| Heart of Algebra | 19 | 26.76 |
| Problem Solving and Data Analysis | 17 | 23.94 |
| Passport to Advanced Math | 16 | 22.53 |
| Additional Topics in Math | 19 | 26.76 |
The Math Test has two parts, one where you can’t use a calculator and one where you can. Most of the questions are multiple choice, but at the end, you have to write the answer in a grid. They’ll give you the everyday formulas you might need.
| Test Breakdown | Calculator Portion | Non-Calculator Portion |
|---|---|---|
| Time allotted | 55 | 25 |
| Total Questions | 38 | 20 |
| Multiple-choice questions | 30 | 15 |
| Grid-in questions | 8 | 5 |
15 Hardest SAT Math Problems:
Category- Non-calculator portion, Grid-in
Question 1: In a right triangle PQR with a right angle at Q, Find the value of tan P.
Ans. Using the relationship between sine, cosine, and tangent in a right triangle. Recall the trigonometric identity:
tan P = sin P / cos P
Since sin R = 4/5, you can find cos R using the Pythagorean identity:
sin^2 R + cos^2 R = 1
(4/5)^2 + cos^2 R = 1
16/25 + cos^2 R = 1
cos^2 R = 1 – 16/25
cos^2 R = 25/25 – 16/25
cos^2 R = 9/25
cos R = sqrt(9/25)
cos R = 3/5
Now, you can find tan P:
tan P = sin P / cos P tan P = (4/5) / (3/5) tan P = (4/5) * (5/3) tan P = 4/3
So, the value of tan P is 4/3.
Question 2: At a lunch stand, hamburgers contain 50 more calories than orders of fries. If a meal with 2 hamburgers and 3 orders of fries adds up to 1700 calories, how many calories are in a single hamburger?
Ans. Let’s use algebra to solve this problem. Let H represent the number of calories in each hamburger, and F represents the number of calories in each order of fries. According to the information given, each hamburger has 50 more calories than each order of fries, so we can write the equation:
H = F + 50
Now, we know that 2 hamburgers and 3 orders of fries have a total of 1700 calories. We can express this as an equation:
2H + 3F = 1700
Now, we have a system of two equations:
- H = F + 50
- 2H + 3F = 1700
We can substitute the value of H from the first equation into the second equation:
2(F + 50) + 3F = 1700
Now, let’s simplify the equation:
2F + 100 + 3F = 1700
Combine like terms:
5F + 100 = 1700
Subtract 100 from both sides:
5F = 1700 – 100 5F = 1600
Now, divide by 5 to find the value of F (the calories in each order of fries):
F = 1600 / 5 F = 320
So, each order of fries has 320 calories. Now, we can find the number of calories in each hamburger using the first equation:
H = F + 50 H = 320 + 50 H = 370
Each hamburger has 370 calories.
Question 3. In triangle ABC, one angle (B) is 90 degrees, and we know the lengths of its sides. Now, we have triangle DEF, which is like triangle ABC but smaller because each side is just one-third the length of the matching side in ABC. What’s the value of sin F in triangle DEF?
Ans. The correct answer is 3/5 or 0.6.
In triangle ABC, since angle B is 90 degrees, it is a right triangle. You can use the Pythagorean theorem to find the length of side AB:
AB^2 = AC^2 – BC^2 AB^2 = 20^2 – 16^2 AB^2 = 400 – 256 AB^2 = 144
Taking the square root of both sides:
AB = √144 AB = 12
Now, you know that the length of side AB is 12 units. In triangle DEF, you mentioned that each side is 1/3 the length of the corresponding side in triangle ABC. Therefore, side DE (corresponding to side AB) has a length of 1/3 * 12 = 4 units.
Now, we have the lengths of sides DE, EF, and DF:
DE = 4
EF = 1/3 * BC = 1/3 * 12 = 12/3
DF = 1/3 * AC = 1/3 * 20 = 20/3
Now, you can find sin F in triangle DEF. Using the definition of sine:
sin F = opposite / hypotenuse
In triangle DEF, angle F is the opposite side EF, and the hypotenuse is side DF.
sin F = EF / DF sin F = (12/3) / (20/3)
Now, simplify:
sin F = (16/3) * (3/20) sin F = (12/20)
Finally, simplify the fraction:
sin F = (4/5)
So, the value of sin F is 3/5.
Question 4: In a right triangle, if one angle measures x degrees and sin(x) = 4/5, Find cos(90° – x°).
Ans. Using the relationship between sine and cosine in a right triangle.
First, recall the trigonometric identity: sin(90° – x°) = cos(x°)
So, to find cos(90° – x°), you can find sin(x°) and then substitute it:
sin(x°) = 4/5
Now, cos(90° – x°) = sin(x°)
Substituting the value of sin(x°):
cos(90° – x°) = sin(x°) = 4/5
So, cos(90° – x°) = 4/5.
Category: Calculator portion, Grid-in
Question 5: How many friends were initially in the group when they decided to split the $800 cost of the trip evenly? Later, when two friends opted out, the remaining friends still divided the $800 equally, resulting in each friend’s share increasing by $20.
Ans. We’ll use ‘n’ to represent the original number of friends in the group.
The initial cost for each friend was calculated as $800 divided by ‘n,’ resulting in the expression 800/n. After two friends decided not to join the trip, the number of friends left to split the $800 cost became ‘n – 2,’ and each friend’s cost was represented by 800/(n – 2).
It’s observed that this new cost represented a $20 increase over the original share. This leads to the equation:
800/n + 20 = 800/(n – 2).
To eliminate the denominators, we multiply both sides of the equation by n(n – 2):
[n(n – 2)][800/n + 20] = [n(n – 2)][800/(n – 2)].
This simplifies to:
800(n – 2) + 20n(n – 2) = 800n.
Now, we have a quadratic equation:
800(n – 2) + 20n(n – 2) = 800n.
Simplify by expanding, simplifying, and collecting like terms:
800n – 1600 + 20n^2 – 40n = 800n.
Combine like terms:
20n^2 – 40n – 1600 = 0.
Factor the quadratic equation, which leads to (n + 8)(n – 10) = 0.
The solutions to this equation are – 8 and 10. Since a negative solution doesn’t make sense in the context of the number of people in a group, we conclude the original number of friends in the group was 10.
Question 6: If Ms. Simon begins her drive at 6:30 a.m., she can maintain her regular driving speed for each part of the journey. However, if she starts her drive at 7:00 a.m., slower traffic causes the travel time from the freeway entrance to the freeway exit to increase by 33%. The travel time for the other two segments remains unchanged. According to the provided table, how many additional minutes will Ms. Simon take to reach her workplace if she starts her drive at 7:00 a.m. instead of 6:30 a.m.? (Round your answer to the nearest minute.)
Ans. Ms. Simon covers a distance of 15.4 miles on the freeway, maintaining an average speed of 50 miles per hour when there’s no traffic delay. So, with no delays, Ms. Simon spends:
(15.4 miles / 50 mph) * 60 minutes/hour = 18.48 minutes on the freeway.
When she departs at 7:00 a.m., her journey becomes 33% longer, which is approximately 6.16 minutes. However, the travel time for the other two segments remains unchanged. Therefore, rounding to the nearest minute, Ms. Simon takes an extra 6 minutes to commute to her workplace when she leaves at 7:00 a.m.
Question 7: Number of Contestants by Score and Day
| Days | 5 out of 5 | 4 out of 5 | 3 out of 5 | 2 out of 5 | 1 out of 5 | 0 out of 5 | Total |
|---|---|---|---|---|---|---|---|
| Day 1 | 2 | 3 | 4 | 6 | 2 | 3 | 20 |
| Day 2 | 2 | 3 | 5 | 5 | 4 | 1 | 20 |
| Day 3 | 3 | 3 | 4 | 5 | 3 | 2 | 20 |
| Total | 7 | 9 | 13 | 16 | 9 | 6 | 60 |
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The table above shows the number of contestants receiving a given score on each day.
What was the mean score of the contestants on Day 1?
Ans. To calculate the mean score of the 20 contestants on Day 1, we add up the total scores of all contestants and then divide it by the number of contestants.
Here’s how we find the total scores for each group of contestants based on the number of correct answers:
2 contestants with 5 correct answers each scored 10 points in total (2 × 5 = 10).
3 contestants with 4 correct answers each scored 12 points in total (3 × 4 = 12).
4 contestants with 3 correct answers each scored 12 points in total (4 × 3 = 12).
6 contestants with 2 correct answers each scored 12 points in total (6 × 2 = 12).
2 contestants with 1 correct answer each scored 2 points in total (2 × 1 = 2).
3 contestants with 0 correct answers scored 0 points in total (3 × 0 = 0).
Adding up all these scores gives us a total of 10 + 12 + 12 + 12 + 2 + 0 = 48 points scored by the 20 contestants. To find the mean score, we divide the total score (48 points) by the number of contestants (20):
Mean score = 48 / 20 = 2.4.
So, the mean score of the contestants is 2.4. This can also be expressed as 12/5 or 2.40.
Question 8: If shoppers enter a store at an average rate of r shoppers per minute and each stay in the store for an average time of T minutes, the average number of shoppers in the store, N, at any one time is given by the formula N = rT. This relationship is known as Little’s law.
The owner of the Good Deals Store estimates that during business hours, an average of 3 shoppers per minute enter the store and that each of them stays an average of 15 minutes. The store owner uses Little’s law to estimate that there are 45 shoppers in the store at any time.
Little’s law can be applied to any part of the store, such as a particular department or the checkout lines. The store owner determines that, during business hours, approximately 84 shoppers per hour make a purchase and each of these shoppers spends an average of 5 minutes in the checkout line. At any time during business hours, how many shoppers, on average, are waiting in the checkout line to make a purchase at the Good Deals Store?
Ans. Little’s law is a mathematical relationship used to estimate the average number of shoppers present in a store at any given moment. This formula is expressed as N = rT, where:
N represents the average number of shoppers in the store at one time.
r denotes the rate at which shoppers enter the store, measured in shoppers per minute.
T signifies the average amount of time each shopper spends inside the store, measured in minutes.
The owner of the Good Deals Store has applied Little’s law to estimate the number of shoppers within the store during their business hours. According to their estimation, an average of 3 shoppers per minute enter the store, and each of these shoppers typically spends 15 minutes shopping. Consequently:
N = 3 (shoppers per minute) * 15 (minutes) = 45 shoppers
This means that the owner estimates there are approximately 45 shoppers inside the store at any given moment during business hours.
Little’s law isn’t limited to the entire store; it can be employed for specific areas like departments or checkout lines. The store owner has analyzed the checkout lines during business hours and found that roughly 84 shoppers per hour complete their purchases. Each of these shoppers spends an average of 5 minutes in the checkout line. To determine the average number of shoppers waiting in the checkout line at any moment during business hours, we apply Little’s law again:
N = 84 (shoppers per hour) * (5 minutes / 60 minutes per hour) = 7 shoppers
Therefore, the owner estimates that, on average, there are about 7 shoppers waiting in the checkout line to make a purchase at the Good Deals Store during their business hours.
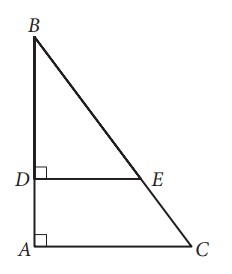
Question 9: In the figure below _ _ _ _ ¾. If _ _ +15 and _ _ = 4, what is the length of _ _?
Ans. Given that tan B = 3/4, we can determine that both triangle ΔABC and triangle ΔDBE are 3-4-5 triangles, which means they are similar to a right triangle with sides of lengths 3, 4, and 5.
Since BC = 15, which is three times the length of the hypotenuse in the 3-4-5 triangle, the similarity ratio between ΔABC and the 3-4-5 triangle is 3:1. Consequently, the length of side AC (opposite angle B) is 3 × 3 = 9, and the length of side AB (adjacent to angle B) is 4 × 3 = 12.
We are also given that DA = 4. Since AB = DA + DB and AB = 12, we deduce that DB = 8. This establishes that the similarity ratio between ΔDBE and the 3-4-5 triangle is 2:1 (DB being the side adjacent to angle B). Therefore, the length of side DE, which is opposite to angle B, is 3 × 2 = 6.



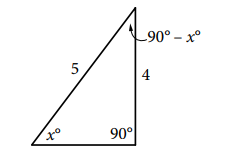














Do SAT Math questions get harder?
Indeed, SAT Math questions typically follow a pattern of increasing difficulty as you progress through the sections. The initial questions are designed to be more straightforward, while the complexity gradually rises, peaking with the last few questions being the most challenging. A helpful strategy is to identify the easier questions and tackle them first, allowing you to build confidence and secure those points before addressing the more demanding ones.
Is it OK to skip questions on the SAT?
In the scoring system for the SAT, you earn one point for each correct answer. However, for every incorrect answer, there is a deduction of 1/4 point. The unique aspect is that you receive no point deductions for questions left unanswered or skipped. This scoring structure encourages strategic decision-making, prompting test-takers to weigh the risk of potential deductions against their confidence in providing a correct response
Is SAT Math easier than SAT English?
This phenomenon is partly attributed to our heavy reliance on calculators in advanced mathematics courses. The widespread use of calculators can impact problem-solving approaches, potentially affecting how students engage with and solve mathematical problems in higher-level courses.