Important Math Formulas Students Should Know

Pure mathematics is, in its way, the poetry of logical ideas

–Albert Einstein, German theoretical physicist

Image Source:https://www.igebra.ai

“Update: This article was last updated on 18th December 2023 to reflect the accuracy and up-to-date information on the page.”

As per a survey, over 93% of adults in the USA feel anxious and uneasy when it comes to dealing with math. So, we can understand how children would feel. That’s why it is important to help students deal with math phobia at the very beginning.

Some children excel at mathematics and can quickly absorb new concepts and formulas, but others are less fluent and may struggle as they go through the grades. We can make the subject more enjoyable for them by assisting them in comprehending the formulas where they get stuck. 

What exactly are math formulas?

These formulas, represented by mathematical symbols, are statements or equations that represent a mathematical relationship or rule. 

Formulas often consist of variables, constants, and operators that describe a mathematical concept or provide a set of rules for solving problems. Some examples of commonly used math formulas include the Pythagorean Theorem, the Quadratic Formula, and the formula for the area of a circle.

There are many important formulas that are worth memorizing. Here are a few examples:

Image Source:https://mathtutory.com

Let’s start with elementary algebra, in which the quadratic formula is used to solve for the roots of a quadratic equation. 

1. The quadratic formula

The word “quadratic” comes from quadrature, the Latin word for square. This is a second-order polynomial equation in a single variable. 

There are three commonly used forms of quadratics:

Standard Form: Standard form: f(x) = ax2 + bx + c, where a ≠ 0

Factored/Intercept Form: y = a (bx +c) (d x+e) 

Vertex Form: y = a ( x − h ) 2 + k 

Image Source:https://www.idtech.com/

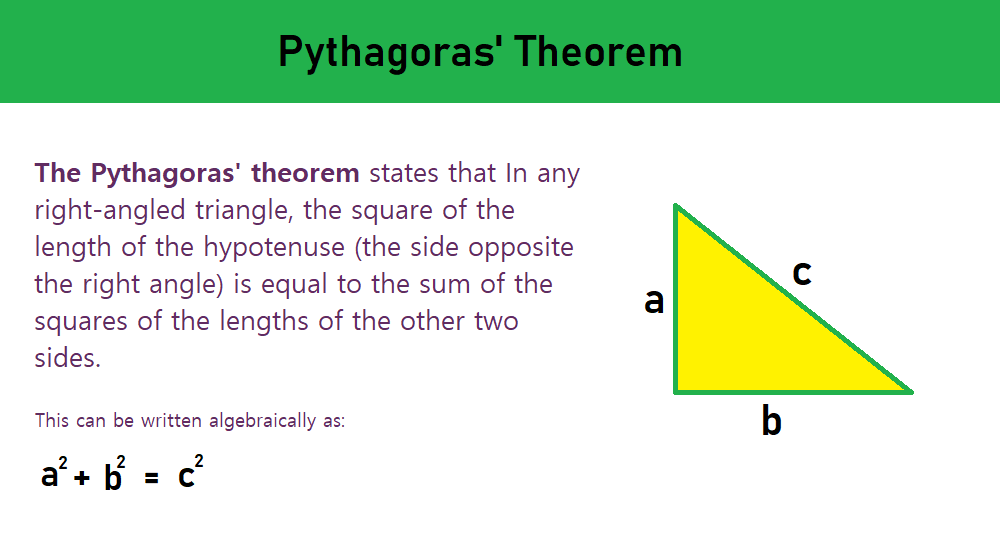                                     Image Source:https://tecadmin.net

2. Pythagorean Theorem

In a right triangle (a triangle with one 90-degree angle), the hypotenuse is the side that is opposite the right angle and is also the longest side of the triangle.

The length of the hypotenuse can be found using the Pythagorean theorem, which states that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. 

The Pythagorean Theorem is written as 

a^2 + b^2 = c^2

a = side of the right triangle

b = side of the right triangle

c = hypotenuse

a and b are the lengths of the other two sides and c is the length of the hypotenuse.

Pythagorean theorem is a useful tool for solving problems involving right triangles, particularly in geometry and trigonometry.

The Pythagorean Theorem is said to be the most famous statement in mathematics.

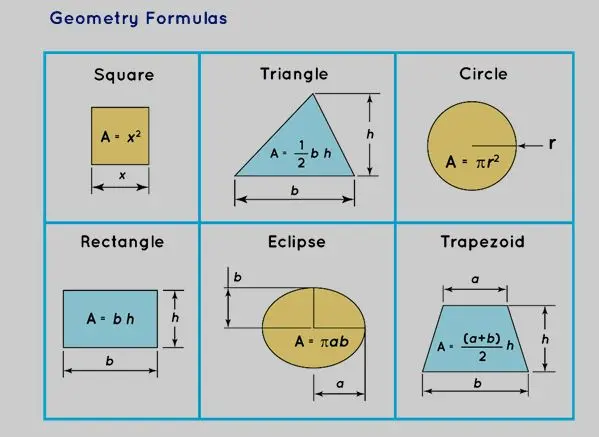Image Source:https://www.pw.live/exams/school/geometry-formula/

2. The Area of a Circle

The formula for the area of a circle with a radius r is:

A = πr2

A = area

r = radius

The formula for the area of a circle is a useful tool for measuring the amount of space occupied by a circular space or object.

If you need to build a tiled roof on a circular wall, you can use the formula to calculate the number of tiles required to cover it completely. 

A) Area

The area of a circle is the space occupied by the circle in a two-dimensional plane. 

Area of the circle formula 

area=πr2

A = area

r = radius

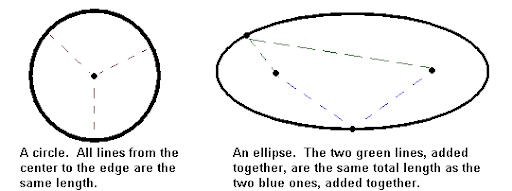
b) Area of an Ellipse

When a circle is stretched in one direction to give it the shape of an oval, it is called an ellipse.

Source: Northwestern University

Ellipse of the circle formula

Ellipse: area=πab

2a and 2b are the lengths of the axes of the ellipse.

3. Area of a Sphere

A sphere is a three-dimensional geometric shape that is completely round, like a ball (football/basketball). A sphere is a set of all points in three-dimensional space that are a fixed distance (called the radius) away from a given point (called the center).

On the other hand, a circle is a two-dimensional shape that can be easily drawn on a piece of paper.

The formula to calculate the surface area of a sphere with radius r is:

A =  V = 4/3 π r³

These formulas are useful for calculating the surface area or volume of a sphere, such as a ball or a planet.

4. Area of a Cylinder

The formula for the volume of a cylinder can be written as:

Volume = Base Area x Height

The base area is calculated as the product of the radius of the base (r) and pi (π), and the height is the distance from the base to the top of the cylinder (h).

So the formula can also be written as:

Volume of a cylinder = πr2h cubic units

This formula can be used to calculate the volume of any cylinder, as long as you know the radius of the base and the height of the cylinder.

5. Area of a Cone

V=πr2h/3

r is the radius of the base 

h is the height

To use this formula, you need to know the radius of the base of the cone and the height of the cone. 

The radius is the distance from the center of the base to the edge of the base, and the height is the distance from the base to the apex (top) of the cone.

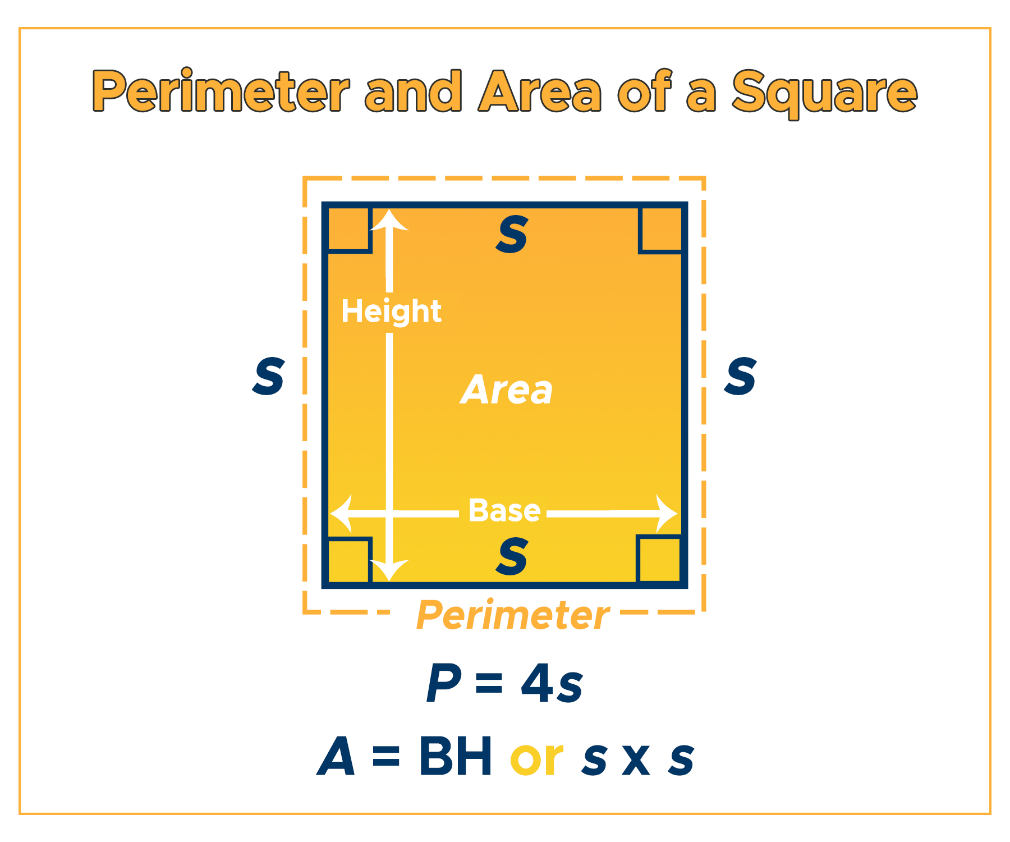Image Source:https://curvebreakerstestprep.com/

6. Area of a square

The formula for the area of a square can be written as:

Area = Side × Side

The formula can also be written as:

Area = Length × Width

Side is the length of one side of the square

Length is the distance along one side of the square

Width is the distance across one side of the square. 

All of these measures are equal for a square since all sides are of equal length.

To use this formula to calculate the area of a square, you need to know the length of one side of the square. Once you have this value, you can multiply it by itself to find the area.

For example, if the length of one side of a square is 5 cm, the area of the square would be:

Area = 5 cm × 5 cm = 25 cm^2

7. Area of a Rectangle

Area = Length × Breadth

Length is the distance along one side of the rectangle

Breadth is the distance across the other side of the rectangle.

To use this formula, you should know the length and breadth of the rectangle. Once you have these values, you can multiply them to find the area.

This formula can be used to find the area of any rectangle as long as you know the length and breadth of the rectangle.

8. Area of a Triangle

Area = (1/2) × Base × Height

The base is the length of the base of the triangle

Height is the distance from the base to the apex (top) of the triangle.

To calculate the area of a triangle, you should know the length of the base of the triangle and the height of the triangle. Once you have these values, you can multiply them together and divide the result by 2 to find the area of the triangle.

Image Source:https://www.igebra.ai/

“Why should we memorize math formulas”?

Just like tables, math formulas come in handy when you are solving problems. Knowing math formulas by heart can boost your confidence and it is especially helpful in high-stakes situations, such as exams or competitions.

There are various reasons why it is important to memorize math formulas. 

✔️Efficiency: You can quickly recall them when you need them, which will save time, especially when solving complex problems or working under time pressure.

✔️Accuracy: Formulas ensure that you have a reliable reference point and can help you avoid mistakes.

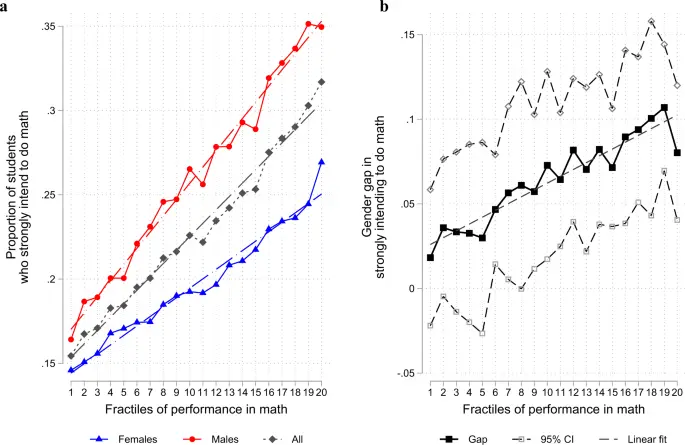Image Source https://www.nature.com

Memorizing math formulas is a useful tool that can help you perform better in math-related tasks and activities. It is an important part of developing a strong foundation in mathematics. In addition to learning math formulas, participating in math competitions can be a great way for students to apply their knowledge, improve problem-solving skills, and build confidence in tackling challenging mathematical problems.

Moonpreneur is empowering the young generation to become future innovators and entrepreneurs by providing them with the world’s education. Keep learning and follow Moonpreneur to get such informative content for your child.

Register your kids in a free advanced math workshop by Moonpreneur for Grades 3rd, 4th, 5th, and 6th.