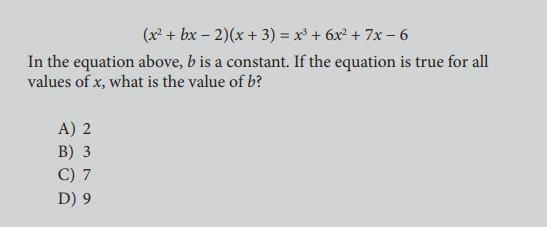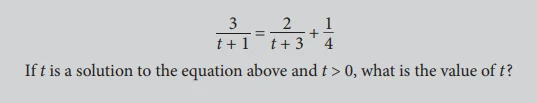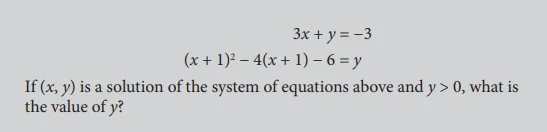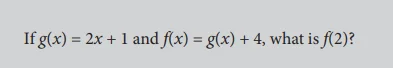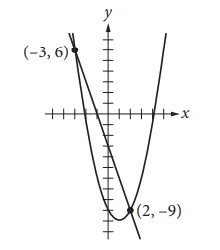The SAT (Scholastic Assessment Test) Passport to Advanced Math questions are designed to test a student’s ability to analyze, rewrite, and manipulate mathematical expressions. They require a strong understanding of algebraic structures and the ability to connect algebraic expressions and graphic data. Students should also be familiar with solving systems of equations that contain both linear and nonlinear equations.
In this blog, we’ll introduce you to the exam and give the best tips and strategies for cracking Passport to Advanced Math questions. We will also mention all the important topics and some popular practice problems asked frequently in the exam.
OVERVIEW OF SAT PASSPORT TO ADVANCED MATH SECTION
The SAT Passport to Advanced Math is a section of the SAT Math test that assesses your readiness for college-level math. The Passport to Advanced Math section focuses on linear equations, functions, and systems. It includes topics such as solving quadratic, linear, and polynomial equations, defining a term or constant and interpreting solutions, creating and using quadratic and polynomial functions, interpreting graphs for quadratic and order-based functions, using an existing graph to identify other equations in a system with a nonlinear equation, creating equivalent algebraic, quadratic, and/or exponential expressions, rewriting simple expressions, and using function notation.
16 of the 58 questions (28%) on the SAT Math Test are Passport to Advanced Math questions.
To prepare for the SAT Passport to Advanced Math questions, students should simplify their tasks by understanding the question, getting comfortable with graphs, and strategizing when solving radical equations. They should also practice solving exponential functions, exponential equations, and exponential expressions, as well as radical equations.
TYPES OF QUESTIONS YOU MAY BE ASKED
Passport to Advanced Math questions build on the knowledge and skills tested on Heart of Algebra questions. Develop proficiency with Heart of Algebra questions before tackling Passport to Advanced Math questions.
2. Quadratic Functions and Equations
Questions in Passport to Advanced Math may require you to build a quadratic function or an equation to represent a context.
Example 2
3. Exponential Functions, Equations, and Expressions and Radicals
Some questions in Passport to Advanced Math ask you to build a function that models a given context.
Example 3
4. Dividing Polynomials by a Linear Expression and Solving Rational Equations
Questions on the SAT Math Test may assess your ability to work with rational expressions, including fractions with a variable in the denominator. This may include the long division of a polynomial by a linear expression or finding the solution to a rational equation.
Example 4
5. Systems of Equations
Solving a system of equations in two variables in which one equation is linear and the other equation is quadratic or another nonlinear equation.
Example 5
6. Relationships Between Algebraic & Graphical Representations of Functions
Some questions in Passport to Advanced Math assess your ability to relate properties of the function f to properties of its graph, and vice versa. You may be required to apply relationships like intercepts, domain range, maximum and minimum values, increasing and decreasing functions, end behavior, asymptotes, symmetry, and transformations.
Example 6
7. Function Notation
You must be able to evaluate a function given the rule that defines it, and if the function describes a context, you may need to interpret the value of the function in the context
Example 7
8. Analyzing More Complex Equations in Context
Equations and functions that describe a real-life context can be complex. Often it is not possible to analyze them as completely as you can analyze a linear equation or function.
Example 8
STRATEGIES FOR PASSPORT TO ADVANCED MATH
Here are some strategies to tackle the Passport to Advanced Math questions with confidence:
1. Utilize multiple-choice options:
Make the most of the multiple-choice format by plugging in answers, trying out different values, or working backward. Eliminate incorrect options to improve your chances of guessing correctly.
2. Be cautious with squaring expressions:
While squaring an expression can be helpful, it can also introduce extraneous solutions or wipe out negatives. Be aware of the implications when squaring or taking a square root.
3. Master laws of exponents and powers:
Understanding how exponents and powers relate is essential for success on the test. Familiarize yourself with these laws, as they are frequently tested and can significantly impact your score.
4. Practice with real SAT questions:
Familiarize yourself with the test format and question types by practicing with real SAT questions. This will help you identify patterns, understand the language used in the questions, and develop strategies for solving problems efficiently.
5. Use a two-pass strategy:
To manage your time effectively, use a two-pass strategy. In the first pass, answer the questions you find easy or straightforward. In the second pass, tackle the more challenging questions. This approach allows you to maximize your points on the easier questions while still having a chance to solve the harder ones.
Additionally, if you have time left after completing the test, you can review your answers and make educated guesses on any remaining questions.
Answer Key for examples above
The solution to Example 1
Solving either of these equations gives b = 3 which is choice B.
To find the value of b, expand the left-hand side of the equation and then collect like terms so that the left-hand side is in the same form as the right-hand side.
(x²+bx-2)(x+3) = (x + bx²-2x) + (3x² + 3bx-6)
= x² + (3+b)x² + (3b-2)x-6
Since the two polynomials are equal for all values of x, the coefficient of matching powers of x should be the same. Therefore,
x^3 + (3 + b)* x^2 + (3b – 2) * x – 6 and x ^ 3 + 6x ^ 2 + 7x – reveals that
3 + b = 6 and 3b – 2 = 7
Example 2 Solution
The left-hand side of the equation can be factored:
2x ^ 2 + 3x – 2 = (2x – 1)(x + 2) = 0
Therefore, either 2x – 1 = 0 which gives gives x = 1/2 or
x + 2 = 0, which gives x = – 2 Since x > 0 the value of x is 1/2
Example 3 Solution
According to the researcher’s estimate, the population is decreasing by 0.6%
each year. Since 0.6% is equal to 0.006, after the first year, the population is
80,000 − 0.006(80,000) = 80,000(1 − 0.006).
After the second year, the population is
80,000(1 − 0.006) − 0.006(80,000)(1 − 0.006)
= 80,000(1 − 0.006)^2
Similarly, after t years, the population will be
80,000(1 − 0.006)^t
according to the researcher’s estimate. This is choice A.
Example 4 Solution
The first step in solving this equation is to clear the variable out of the denominators by multiplying each side by (t + 1)(t + 3)
This gives 3(t + 3) = 2(t + 1) + 1/4 * (t + 1)(t + 3)
Now multiply each side by 4 to get rid of the fraction:
12(t + 3) = 8(t + 1)(t + 3)
Expanding all the products and moving all the terms to the right-hand side gives
0 = t ^ 2 – 25
Therefore, the solutions to the equation are t = 5 and t = – 5 Since t > 0 the value of t is 5.
Example 5 Solution
The structure of the second equation suggests that (x + 1) is a factor of the first equation.
Subtracting 3x from each side of the first equation gives you y = – 3 – 3x
which can be rewritten as y = – 3(x + 1) .
Substituting – 3(x + 1) for y in the second equation gives you
(x + 1) ^ 2 – 4(x + 1) – 6 = – 3(x + 1) which can be rewritten as
(x + 1) ^ 2 – (x + 1) – 6 = 0
The structure of this equation suggests that x + 1 can be treated as a variable.
Factoring gives you ((x + 1) – 3)((x + 1) + 2) = 0 or (x – 2)(x + 3) = 0
Thus, either x = 2 which gives y = – 3 – 3(2) = – 9 or x = – 3 which gives
y = – 3 – 3(- 3) = – 9
Therefore, the solutions to the system are (2,-9) and (-3, 6). Since the question states that y > 0 the value of y is 6.
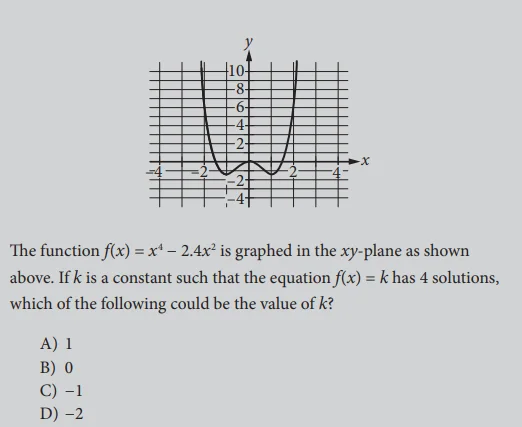
Example 6 Solution
Choice C is correct. The equation f(x) = k will have 4 solutions if and only if
the graph of the horizontal line with equation y = k intersects the graph of f
at 4 points. The graph shows that of the given choices, only for choice C, −1,
does the graph of y = −1 intersect the graph of f at 4 points.
Example 7 Solution
You are given f(x) = g(x) + 4 and therefore f(2) = g(2) + 4 To determine the value of g(2), use the function g(x) = 2x + 1 Thus, g(2) = 2(2) + 1 and g(2) = 5
Substituting g(2) gives f(2) = 5 + 4 or f(2) = 9
Example 8 Solution
Choice C is correct.
If the mass of the object is halved, the new mass is m/2.
If the speed of the object is doubled, its new speed is 2v.
Therefore, the new kinetic energy is ½ (m/2)(2v)²= 1/2(m/2)(4v²)= mv²
This is double the kinetic energy of the original object, which was 1/2mv².
CONCLUSION
The SAT Passport to Advanced Math questions are not designed to be tricky, but rather to test a student’s ability to apply their mathematical knowledge to complex problems. Students should not be afraid to guess if they are truly stuck, but they should also take the time to fiddle around with the problem and try out different strategies before giving up. With practice and preparation, students can improve their skills and confidence in this area of the SAT Math test.
Moonpreneur understands the needs and demands this rapidly changing technological world is bringing with it for our kids. Our expert-designed Advanced Math course for grades 3rd, 4th, 5th, and 6th will help your child develop math skills with hands-on lessons, excite them to learn, and help them build real-life applications.
Register for a free 60-minute Advanced Math Workshop today!